Incorporate Bregman Divergence to generalize fGAN

一、Fenchel Legendre

Fenchel Duality和Legendre变换本质上是一样的，只是从不同的角度去解释，它描述了函数斜率与截距之间的关系。

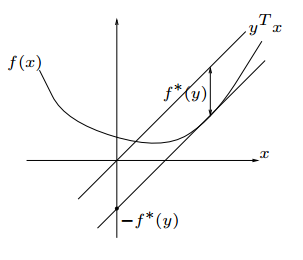如上左图，过原点作一条斜线\(y=kx\)，将其向下平移与\(f(x)\)相切，该切线与\(y\)轴的截距与斜线向下平移的距离相等，\(f^*(k)是截距\):

\[f^*(k) = kx-f(x)\] \[f'(x)=k\]

这就是Legendre变换，它要求\(f(x)\)①可导（\(f'(x)=k\)） ②凸函数（函数具有唯一性）。 Fenchel突破了凸可导的限制，将上述两个等式换成一个更general的表达式：

\[\begin{align} f^*(t) = \max_x\{xt-f(x)\} \\ \end{align}\]

\(f^*(t)\)称为\(f(x)\)的共轭。这样我们可以理解为函数是无数切线切出来的一个曲线。

例：求\(g(x) = \log(1+e^x)\)的共轭\(g^*(y)\)

切线斜率\(y = \frac{e^x}{1+e^x} \in (0,1)\),\(e^x = \frac{y}{1-y},x = \log \frac{y}{1-y}\)
\[g(x)=\log(1+e^x)=\log \frac{1}{1-y}\]

\[\begin{split} g^*(y) &= yx-g(x) \\ &= y\log \frac{y}{1-y}-\log \frac{1}{1-y} \\ &= y\log y +(1-y) \log(1-y) \end{split}\] \[\therefore g^*(y)=\left\{\begin{matrix} y\log y +(1-y) \log(1-y) &\quad y\in (0,1)\\ 0 &\quad otherwise \end{matrix}\right.\]

Fenchel共轭的性质：

共轭的共轭等于原函数\(g^{**}(x) = g(x)\)
\(g(x)\)是凸函数，那么共轭\(g^*(x)\)也为凸函数
\(g(x)\)是\(L-smooth\),那么\(g^*(x)\)是\(\frac{1}{L}-SC(Strongly Convex)\)

二、f-GAN

f-GAN: Training Generative Neural Samplers using Variational Divergence Minimization

\[\begin{align} &f^*(t) = \max_x\{xt-f(x)\} \quad (f^*(t))'=x \\ \Leftrightarrow &f(x) = \max_t\{xt-f^*(t)\}\quad f'(x)=t \end{align}\]

给定\(\,x\,\)和函数\(\,f\,\)找到一个最优的\(\,t\,\)使得\(\,xt-f^*(t)\,\)最大。

\[D_f (P||Q)=\int_{x}q(x)f(\frac{p(x)}{q(x)})dx\\\]

f-Divergence中\(\,f\,\)为凸函数且\(f(1)=0\,\). 判别器\(\,D\,\)的目标是最大化上式，而上式变量并不含\(\,D\,\)，可以利用Fenchel共轭对其进行变换,将\(\,t\,\)换成\(\,D(x)\,\)作为优化对象：

\[\begin{align} D_f (P||Q) &=\int_{x}q(x)f(\frac{p(x)}{q(x)})dx\\ &= \int_{x}q(x) \max_t \{ \frac{p(x)}{q(x)} t - f^*(t)\} dx \\ & \geq \int_{x}q(x) \{ \frac{p(x)}{q(x)} D(x) - f^*(D(x))\} dx\\ & = \int_{x} p(x) D(x) - q(x) f^*(D(x)) dx\\ \end{align}\] \[\begin{align} \therefore D_f (P||Q) &\approx \max_D \int_{x} p(x) D(x) - q(x) f^*(D(x)) dx \quad (*)\\ &\approx E_{x\sim P} [D(x)] - E_{x\sim Q} [ f^*(D(x))] \end{align}\]

\((*)\,\)式中可以简化为最大化\(\,p(x) D(x) - q(x) f^*(D(x)) \,\),我们令\(p(x)=A,q(x)=B,D(x)=X\),对\(\,D(x)\,\)进行求解：

\[\begin{align} \max_D \quad &p(x) D(x) - q(x) f^*(D(x)) \\ &\rightarrow A-B(f^*(X))'=0\\ &\rightarrow (f^*(X))'=\frac{A}{B}=\frac{p(x)}{q(x)}\\ &\rightarrow f'(\frac{p(x)}{q(x)})=X=D(x) \end{align}\]

训练判别器过程中，GAN的\(D(x)\)最优取\(\,\frac{p(x)}{p(x)+q(x)}\,\),f-GAN中\(D(x)\)最优取\(f'(\frac{p(x)}{q(x)})\,\),当\(\,f(x)=x\log x - (x+1)\log (x+1)\)时为GAN。

三、b-GAN

B-GAN: UNIFIED FRAMEWORK OF GENERATIVE ADVERSARIAL NETWORKS

1. Bregman Divergence

\[B_f(A,B) = f(A) - f(B) - f'(B)(A-B)\]

2. bGAN

假设有两个分布\(p(x)\)和\(q(x)\), 真实的密度比\(r(x)=\frac{p(x)}{q(x)}\),模型的密度比为\(r_\theta(x)\), \(\theta\)为模型的参数。

\[\begin{align} BD_f(r||r_\theta) &= E_{x\sim Q}[B_f(r,r_\theta)] \\ &= \int (f(r(x)) - f(r_\theta(x)) - f'(r_\theta(x))(r(x)-r_\theta(x)))q(x)dx \end{align}\]

\(r(x)\)为常数，可以去除无关项只保留\(r_\theta\)相关项：

\[\begin{align} BR_f(r_\theta) &= \int (- f(r_\theta(x)) - f'(r_\theta(x))(r(x)-r_\theta(x)))q(x)dx \\ &= \int (f'(r_\theta(x)) r_\theta(x) - f(r_\theta(x)))q(x)dx - \int f'(r_\theta(x)) p(x) dx \\ &= E_{x\sim Q} [f'(r_\theta(x)) r_\theta(x) - f(r_\theta(x))] - E_{x\sim P} [f'(r_\theta(x))] \end{align}\]

目标是最小化上式的密度比估计，换成下式就和fGAN有相同的形式, \(D(x) = f'(r_\theta(x))\)

\[\begin{align} \max_{r_\theta} &E_{x\sim P} [f'(r_\theta(x))] - E_{x\sim Q} [f'(r_\theta(x)) r_\theta(x) - f(r_\theta(x))] \\ \rightarrow \max_D &E_{x\sim P} [D(x)] - E_{x\sim Q} [ f^*(D(x))] \end{align}\]

可以看出\(Bregman Div\)和fGAN之间存在对偶关系。

四、 scaled-Bregman GAN

BreGMN: scaled-Bregman Generative Modeling Networks

\[\begin{align} B_f(P,Q) &= \int_{\chi } f(p(x)) - f(q(x)) - f'(q(x))(p(x)-q(x)) dx\\ B_f(P,Q|M) &= \int_{\chi } f(\frac{p(x)}{m(x)}) - f(\frac{q(x)}{m(x)}) - f'(\frac{q(x)}{m(x)})( \frac{p(x)}{m(x)} - \frac{q(x)}{m(x)})dM \\ &= \int_{\chi }B_f(\frac{p(x)}{m(x)},\frac{q(x)}{m(x)})\:m(x)dx \end{align}\]

上式和bGAN很相似，bGAN是\(\int_{\chi }B_f(\frac{p(x)}{q(x)},r_\theta(x))\:q(x)dx\). 下面我们令\(m(x)=q(x)\)

\[\begin{align} B_f(P,Q|M) &= \int_{\chi } (f(\frac{p(x)}{q(x)}) - f(1) - f'(1)( \frac{p(x)}{q(x)} - f(1)))q(x)dx \\ &= \int_{\chi }f(\frac{p(x)}{q(x)})q(x)dx \quad (f(1)=0,f'(1)=0) \end{align}\]

这样就得到f-Divergence,它要求\(f(1)=0\),\(f(x)\)为凸函数且\(f(x)\geq 0\)则\(f'(1)=0\)

五、总结

Method	Div in Bregman form	Estimate D(x)
\(GAN\)		\(\frac{p}{p+q}\)
\(fGAN\)	\(\int B_f(\frac{p(x)}{q(x)},1)q(x)dx\)	\(f'(\frac{p}{q})\)
\(bGAN\)	\(\int B_f(\frac{p(x)}{q(x)},r_\theta(x))q(x)dx\)	\(\begin{align} &r(x) =\frac{p(x)}{q(x)}\\ Dual\, &relation\, with \,fGAN \end{align}\)
\(BreGMN\)	\(\int B_f(\frac{p(x)}{m(x)},\frac{q(x)}{m(x)})m(x)dx\)