Energy-based GAN | Tingting Liao

0. Evidence Lower Bound ELBO

最大似然可以推导出最大ELBO

\[\begin{align} \log p(x) &= \int_z q(z) \log p(x) dz \\ &= \int_z q(z) \log \frac{p(x,z)}{p(z|x)} dz \\ &= \int_z q(z) \log \frac{p(x,z)}{q(z)} \frac{q(z)}{p(z|x)}dz \\ &= \int_z q(z) \log (\frac{p(x,z)}{q(z)}) dz+KL(q(z)||p(z|x)) \\ &= L_b +KL(q(z)||p(z|x)) \\ \end{align}\]

记$L_b = \int_z q(z) \log (\frac{p(x,z)}{q(z)}) dz$ 就是evidence lower bound, 当$KL(q(z),p(z\| x))=0$时，最大似然就等价于ELBO，最大似然就是最小化模型生成分布 $p(z\|x)$ 和真实分布 $q(z)$ 之间的KL距离。

1. VAE

AE将输入encode成中间编码 $z$ 再将其还原decode成 $\hat{x}$, 它的局限性在于编码需要根据输入得到，随意输入一个中间编码生成图片可能会很奇怪。那么我们能否得到输入数据 $X$的分布$p(x)$，然后在 $p(x)$中采样生成图片即可。任何一个分布都可以看作是多个高斯分布的叠加。

\[p(x)=\int_z p(x|z)p(z)dz\\\]

和混合高斯不一样的是， $z$ 服从连续分布。如果我们知道$z$ 的分布那么就可以得到与输入近似的 $\hat{x}$,这相当于是一个decode的过程， $z$ 的分布则可以通过encode输入得到。有两个encoder，一个encoder输出均值 $\mu$ ,另一个输出方差 $\sigma$, 这样就能得到 $p(z\|x)$的分布 $N(\mu, \sigma^2)$ ,从 $p(z\|x)$中采样得到 $z$ . 这里有两个问题：

$z$ 为什么是从$p(z\|x)$中采样的而不是从 $q(z)$中采样的？
采样得到的 $z$与真实数据的编码会有一定的误差如何解决？

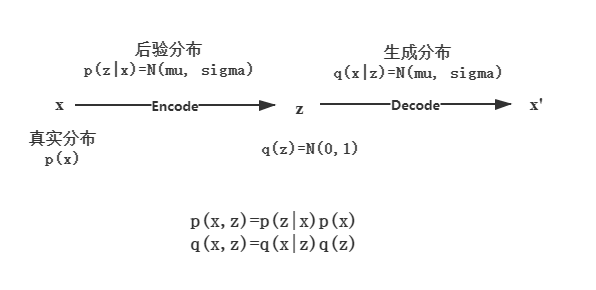
第一个问题：p(z|x)和 q(z)是同分布的.

\[p(z) = \int p(z|x)p(x) dx=N(\mu, \sigma^2)\int p(x)dx = N(\mu, \sigma^2)\]

第二个问题：假设$q(z)$理想情况下服从正态分布 N(0,1) ，让 p(z|x) 逼近正态分布，这样就能让采样的 z 接近理想编码分布。

\[\min KL(p(z|x)||q(z))\]

VAE的优化目标是最小化 $KL(p(x,z) \| q(x,z))$，它等价于最大化ELBO.

\[\begin{align} KL(p(x,z) || q(x,z)) & = \int \int p(x,z) \log \frac{p(x,z)}{q(x,z)}dzdx\\ & = \int \int p(z|x)p(x) \log \frac{p(z|x)p(x)}{q(x|z)q(z)}dzdx\\ & = E_{x\sim p(x)} [ \int_z p(z|x)\log \frac{p(z|x)p(x)}{q(x|z)q(z)}dz]\\ & = E_{x\sim p(x)} [\int_z p(z|x)\log \frac{p(z|x)}{ q(z)}dz + \int_z p(z|x)\log \frac{p(x)}{ q(x|z)}dz ]\\ & = E_{x\sim p(x)} [KL( p(z|x)||q(z))-\int_z p(z|x) \log q(x|z)dz + p(x) ]\\ & \rightarrow KL( p(z|x)||q(z))-\int_z p(z|x) \log q(x|z)dz + C \\ & \rightarrow KL( p(z|x)||N(0,1))-E_{z \sim p(z|x) }[\log q(x|z)] \end{align}\]

第一项为KL正则项，第二项为重构损失(给定编码器 $p(z\|x)$的情况下解码器$p(x\|z)$的值尽可能高）。所以VAE可以看作是加了KL正则的Auto-Encoder。

VAE在重构损失的基础上，最大化ELBO，它的目的是最大化似然，等价于最小化生成分布 $p(z\|x)$ 和编码真实分布 $q(z)$ 之间的KL距离，并假设 $q(z)$ 服从标准正态分布。

2. Energy-Based GAN

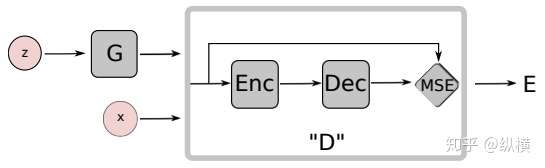
生成器 $G$ 将 $z$ 作为输入，输出 $\hat{x}= G(z)$

判别器 $D$ 是一个Auto-encoder, 输出重构误差 $D(x)=\|Dec(Enc(x))-x\|$。那么 $D$ 目标函数应该让 $D(x)$ 尽可能大，让 $D(G(z))$ 尽可能小。$G$ 的目标是最大化 $D(G(z))$

\[\begin{align} L_D(x,z)&=D(x)-D(G(z))\\ L_G(z)&=D(G(z)) \end{align}\]

那么这和能量有什么关系？ 生成器就是一个能量函数，输出的能量值 $D(x)$ 低就将它分类为real, 能量值高就分类为fake, 对应了上面的重构损失。

2.1 能量判别器

定义能量函数 $U_{\theta}(x), \theta$是能量函数的参数，系统总能量 $Z_\theta = \int e^{-U_{\theta}(x)}dx$, 样本概率和能量之间关系表示为：$p_{\theta}(x) = \frac{e^{-U_{\theta}(x)}}{Z_{\theta}} \propto e^{-U_{\theta}(x)}$,最大似然目标函数

\[\max_\theta \prod_{x\in X} p_\theta(x) \\\]

上式取对数除以 $N$ （输入样本个数），目标函数变成 $\max_\theta E_{x\sim p_D} [\log p_\theta(x) ],p_D$表示 $X$ 的真实分布。

\[-\log p_\theta(x) = U_\theta(x) + \log Z_\theta \\\] \[\begin{aligned} -\frac{\partial \log p_\theta(x) }{\partial\theta }&= \frac{\partial U_\theta(x)}{\partial\theta } + \frac{1}{Z_\theta }\frac{\partial Z_\theta }{\partial \theta}\\ &= \frac{\partial U_\theta(x)}{\partial\theta } + \frac{1}{Z_\theta } \int -e^{-U_\theta(x)} \frac{\partial U_\theta(x)}{\partial \theta }dx\\ &= \frac{\partial U_\theta(x)}{\partial\theta } - E_{x\sim p(x)}[\frac{\partial U_\theta(x)}{\partial \theta}] \end{aligned}\\\]

最大然就变成了最小化下式：

\[\begin{aligned} & \frac{\partial E_{x\sim p_D} [-\log p_\theta(x) ] }{\partial \theta} \\ \rightarrow & E_{x\sim p_D} [\frac{\partial U_\theta(x)}{\partial\theta }] - E_{x\sim p_{\theta}(x)}[\frac{\partial U_\theta(x)}{\partial \theta}] \end{aligned}\]

$p_D$是真实分布, $p_\theta$是模型近似出来的假分布.最大似然就变成找到一组最优的参数使得真实分布和假分布之间的能量$U_\theta(x)$越近越好。目标函数为：

\[\begin{aligned} &\min_\theta E_{x\sim p_D} [U_\theta(x)] - E_{x\sim p_{\theta}(x)}[U_\theta(x)] \\ \rightarrow &\min_\theta E_{x\sim p_D} [D(x)] - E_{x\sim p_{\theta}(x)}[D(x)] \\ \end{aligned}\]

可以看到可以用生成器 $D$ 来替代能量函数 $U_\theta$ 。但是这个公式和EBGAN的目标函数不完全一样，因为用判别其作为能量函数之后， $\theta$ 应该与 $D$ 的参数 $W$ 是一致的, 所以 $x\sim p_\theta (x)$ 不能直接替换成生成器 $p_G$ 的采样。那么如何从 $p_\theta$ 中采样 $x$ ,即如何得到假样本？

2.2 最大熵生成器

用生成器 $G$ 的生成分布 $p_G$ 近似替代 $p_\theta$，并使两分布距离尽可能的小以减小近似误差

\[\begin{align} \min_G KL(p_G||p_\theta) &= p_G \log \frac{p_G}{p_\theta}\\ &= p_G \log p_G - p_G \log p_\theta\\ &= -H[p_G] - E_{p_G}[\log p_\theta]\\ &= -H[p_G] + E_{p_G}[U_\theta(x)] +\log Z_\theta \end{align}\]

上式中$\log Z_\theta$和$G$无关，那么生成器的目标函数就变成了,从$p_G$中采样$x$相当于是从先验分布$p(z)$采样$z$经过生成器得到的$G(z)$:

\[\begin{align} &\min_G -H[p_G] + E_{x\sim p_G}[U_\theta(x)]\\ \rightarrow &\min_G -H[p_G] + E_{z\sim p(z)}[U_\theta(G(z))] \end{align}\]

EBGAN的生成器目标函数是最小化生成样本的能量，这里在EBGAN的基础上多了一项，最大化生成分布的熵 $H[p_G]$ 。

接下来问题是如何计算 $H[p_G]$ ? 这部分证明需要互信息(mutual information)的信息。

2.3 互信息(mutual information)

互信息是两个变量之间共有的信息。定义为：

\[\begin{align} I(X,Y)&=\int_X \int_Y p(X,Y)\log \frac{p(X,Y)}{p(X)p(Y)}\quad(*)\\ &=KL(p(X,Y)||p(X)p(Y)) \end{align}\]

它有以下4条性质：

1）当$X,Y$相互独立时，$p(X,Y) =p(X)p(Y),I(X,Y)=0$互信息为零

2）当$X,Y$不独立时，$(*)$式可以推导简化为：

\[I(X,Y)= H(X) - H(X|Y)\]

$H(X)$为$X$的熵，即$X$的不确定度，

$H(X\|Y)$为已知 $Y$ 的情况下$X$ 的不确定度，

$I(X,Y)$为已知 $Y$ 的情况下$X$ 不确定度减少的部分，减少的这部分就是 $X$和$Y$ 的共同信息产生的。或者从 $KL$ 的角度也可以理解为，$I(X,Y)$ 计算了$(X,Y)$的联合分布与两者边缘分布乘积之间的$KL$ 距离，也就是$X,Y$ 的共有部分。

3）$I(X,Y)\geq 0$

4) 当$X,Y$知道一个就能推出另一个时，$I(X,Y)=H(X)=H(Y)$

生成器中，我们希望输入和输出之间的互信息 $I(G(Z),Z)$ 尽可能的大，根据性质4）可以得到

\[\begin{aligned} I(G(Z),Z) &= H(G(Z)) - H(G(Z)|Z)\\ &= H(G(Z)) \end{aligned}\]

最大化互信息 $I(G(Z),Z)$ 等价于最大熵 $H(p_G)$，我们用 $KL(p(\hat{x}\|z)p(z)\|p(\hat{x})p(z))$ 来优化。但是$KL$ 散度是没有上限的，更好的做法是用$Jensen-Shanno$ 散度，$JSD$是对称的$KL$散度，它有上界而且可以达到同样的效果。而在GAN Theory理论推导中，判别器的目标函数等价于最大化$JS$

\[\begin{align} &\max_D E_{x\sim p_D}[\log D(x)] + E_{x\sim p_G}[\log (1-D(x))]\\ \rightarrow & \max JSD(p_D,p_G) \end{align}\]

因此将 $p_D,p_G$ 换成 $p(\hat{x}\|z)p(z),p(\hat{x})p(z)$ 目标函数就变成：

\[\begin{align} I_{JSD}=\max_D E_{(x,z)\sim p(\hat{x}|z)p(z)}[\log D(x,z)] + E_{(x,z)\sim p(\hat{x})p(z)}[\log (1-D(x,z))]\\ \end{align}\]

综上GAN的能量模型损失函数为：

\[\begin{align} L_G &= -I_{JSD}(G(Z),Z) + E_{z\sim p(z)}[D(G(z))]\\ L_D&= E_{x\sim p_D}[D(x)]-E_{z\sim p(z)}D(G(z)) \end{align}\]