MirrorGS
Incorporating Mirror Reflections into 3D Gaussian Splatting
I reimplement Mirror3DGS
Key Idea
For non-mirron area, rendering image from the origin camera viewpoint.
For mirror area, transforming the camera to the other side of the mirror.
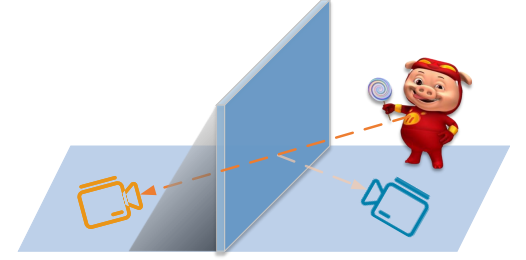
To render the mirror area, we have to solve two problem:
- How to get the mirror plane from the scene?
- How to transform the camera?
1. Mirror Plane Estimation
Mirror Label Learning
To get the mirror points, we can learn a mirror label \(k \in [0, 1]\) for each guassian point. To learn the mirror labels, mirror masks are required for supervision.
\[\mathcal{L}_{mirr\_mask}=\mathcal{L}_1(\mathbf{M} , \mathbf{M} _{gt})\]The mirror mask rendering is similar to rgb image rendering, replacing color with $k$. During training, the mirror points can be extracted through a threshold. Then estimate the plane equation from the mirror points.
Plane Fitting
\[ax + by + cz + d = 0\]Where \(n=(a, b, c)^⊤\) is the normal of the plane, \(d\) is the distance to the origin. Assuming for any point \(p = (x, y, z)^⊤\) on the plane satisfies:
\[n^{T}p+d=0\]The objective is to minimizing the least squares error:
\[\sum_{i=1}^{m} (n^T(p_i - \mathbf{c}))^2\]where \(\mathbf{c} = \frac{1}{m} \sum_{i=1}^{m} \mathbf{p}_i\), \(d=-n^T\mathbf{c}\) and normal \(n\) equals the eigenvector of the smallest eigenvalue of the covariance matrix:
\[\sum_{i=1}^{m} (\mathbf{p}_i - \mathbf{c})(\mathbf{p}_i - \mathbf{c})^T\]The method is simple yet effective for clean points. However, the extracted points are noisy. Thus we use the RANSAC algorithm
2. Mirror Camera Transformation
The camera transformation is