近端梯度下降

1. 满足Lipschitz连续的梯度下降

\[\begin{split} f(x^{k+1})& \geq f(x^k)+\left \langle f'(x^k),x^{k+1}-x^k\right \rangle+\frac{L}{2}||x^{k+1}-x^k||^2\\ &\geq \frac{L}{2}||(x^{k+1}-x^k)+\frac{1}{L}f'(x^k))||^2+\Phi(x^k) \end{split}\]

将不等式右边拆分成关于\(x^{k+1}\)的项，其它关于\(x^k\)为无关项写成\(\Phi(x^k)\)

\[\begin{split} &\min_{x^{k+1}} f(x^{k+1})\\ = \quad& \min ||(x^{k+1}-x^k)+\frac{1}{L}f'(x^k))||^2\\ \therefore \quad &x^{k+1} = x^k - \frac{1}{L}f'(x^k) \end{split}\]

在满足Lipchitz连续的下降算法中，步长取\(t=\frac{1}{L}\)，在上一篇博客中也有写到,将该函数推广到任意可导函数，步长为\(\alpha\)，即为一般的梯度下降。

2. 近端梯度下降Proximal gradient descent

\(PG\)主要针对损失函数中有不可导的函数的梯度下降问题，其中\(h(x)\)为不光滑的凸函数如\(L_1\)正则.

\[\min_x f(x)+ \lambda h(x)\]

根据上节推导有：

\[\begin{split} f(x^{k+1})=\frac{L}{2}||(x^{k+1}-x^k)+\frac{1}{L}f'(x^k))||^2+\Phi(x^k) +\lambda ||x^{k+1}||_1 \end{split}\]

令\(z = x^k - \frac{1}{L}f'(x^k)\)，则优化变成：

\[x^{k+1} = prox_{\lambda h(x)}=\min_x \frac{1}{2t}||x-z||^2+\lambda ||x||\]

这里将\(z\)看作常数，根据求\(f(x)\)的导数得到\(z\),然后目标变成找一个最优的\(x^*\)使得上式最小。即0属于上式导数的区间内【不理解这句话建议先看次梯度】：

\[0 \in \frac{1}{t}(x^*-z)+\lambda \partial |x^*|\]

其中： \(\partial |x^*|= \left\{\begin{matrix} 1 \quad &x^*>0\\ [-1,1] \quad &x^*=0\\ -1 \quad &x^*<0 \end{matrix}\right.\)

那么：

\[\begin{split} &x^*>0，0=\frac{1}{t}(x^*-z)+\lambda，\therefore x^*=z-t\lambda>0 \\ &x^*<0，0=\frac{1}{t}(x^*-z)-\lambda，\therefore x^*=z+t\lambda<0 \\ &x^*=0，0 \in [\frac{1}{t}(x^*-z)-\lambda,\frac{1}{t}(x^*-z)+\lambda]，\therefore x^*=0 \end{split}\]

因此：

\[x^* =\left\{\begin{matrix} z-t\lambda \quad &z>t\lambda \\ 0 \quad &-t\lambda<z<t\lambda \\ z+t\lambda \quad &z<-t\lambda \end{matrix}\right.\] \[prox_{\lambda h(x)}=\max\{|z|-t\lambda,0\}\]

总结

近端梯度下降主要分为两步：1）沿着\(f(x)\)梯度方向找到点\(z\)；2)优化\(h(x)\)

\[\begin{split} &Gradient Step:z = x^k - tf'(x^k) \\ &Proximal Step:x_{k+1} = \max\{|z|-t\lambda,0\} \end{split}\]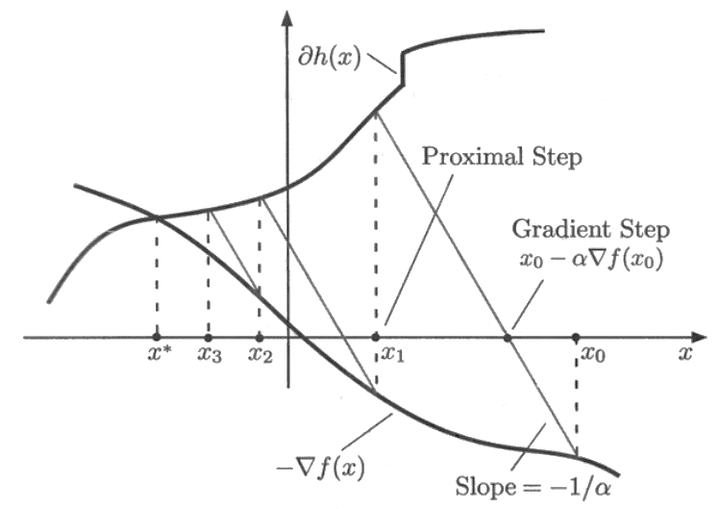

该图中所表示的意思其实是：

\[\begin{split} &\min_x \frac{1}{2\alpha}||x-z||^2+h(x) \\ \Rightarrow& \frac{1}{\alpha}(x-z)+\partial h(x)=0 \end{split}\]

即\(x\)为\(\left\{\begin{matrix} y_1&= -\frac{1}{\alpha}(x-z)\\ y_2&=\partial h(x) \end{matrix}\right.\)两线交点，\(y_1\)为图中斜率为\(-\frac{1}{\alpha}\)斜线，该线经过点\((x_k, -\frac{\triangledown f(x_k)}{\alpha})\)【图中\(- \triangledown f(x)应写成-\frac{\triangledown f(x)}{\alpha}\)】，\(y_1\)与横坐标的交点即为Gradient Step的\(z\)，与\(y_2=\partial h(x)\)为Proximal Step最终的解.

近端梯度下降的收敛速度与梯度下降类似，假设\(f(x)\)满足\(L-Lipschitz\)且\(h(x)\)为凸函数，固定步长\(t\),\(PG\)满足：

\[f(x^k)-f(x^*)\leq \frac{||x_0-x^*||_2}{2tk}\]

收敛速度为\(O(\frac{1}{\epsilon})\)

3. 投影梯度下降Projected gradient descent

对于有约束的凸函数：

\[\min_{x\in S} f(x)\]

每次梯度下降需要将计算后的值拉回到约束域\(S\)中去

\[y_{k+1} = x_k - \eta \triangledown f(x_k)\] \[x_{k+1} = \min_{x\in S} ||x-y_{k+1}||^2_2\]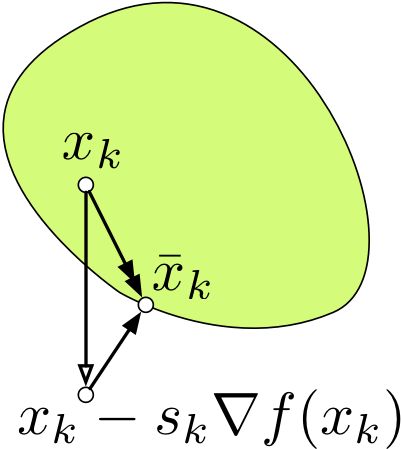

若梯度更新后的值不在\(S\)内，那么将其拉回到\(S\)中最近的点,即图中的\(\overline{x}_k\)。

\(PD\)的第二步优化可以近似的看成是一次投影,找到一个距离\(z\)较近的点，使得\(h(x)\)尽可能的小。

\[\min_x \frac{1}{2t}||x-z||^2+h(x)\] \[\min D(x,z)+h(x)\]

4. 镜像梯度下降Mirror descent

投影算法和\(PD\)都是计算欧式距离，而镜像梯度下降的贡献主要在于定义了一个更一般的距离而不仅仅是欧式距离我们称之为Bregman散度，它包含了对一切距离的定义。

Bregman divergence 以下来源于这里。欧式距离：

\[\begin{split} d^2(x,y)&=\sum_{i=1}^{n}(x_i-y_j)\\ d^2(x,y)&=||x||^2-||y||^2-\left \langle 2y,x-y\right \rangle \end{split}\]

令\(f(x)=x^2\)时，上式变为:

\[B(x,y)=f(x)-(f(y)+\left \langle \triangledown f(y),x-y\right \rangle)\]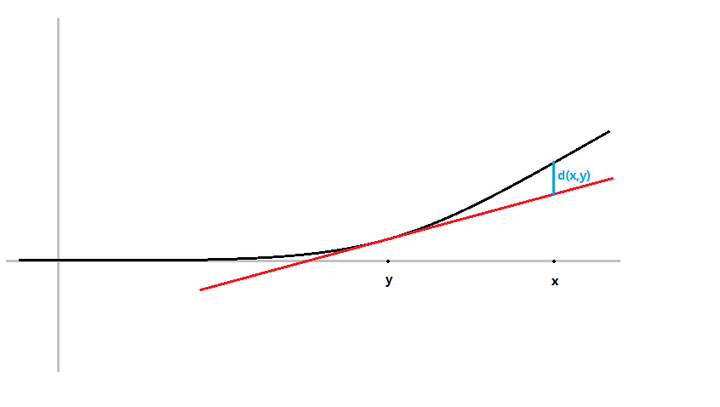

\(f(y)+\left \langle \triangledown f(y),x-y\right \rangle)\)为函数\(f(x)=x^2\)在\(y\)点切线在\(x\)处的取值，所以欧式距离可以表示为图中蓝线部分。而距离必须满足非负\(d(x,y)\geq 0\),那么\(f\)必须在其切线的上方,也就是说函数\(f\)是凸函数.
\(\quad\)因此我们可以将欧式距离函数\(f(x)=x^2\)换成其它距离的凸函数，如:

【\(Mirror Descent\)三点性质】:

\[\begin{split} ||x_{k+1}-x^*||^2 &=||x_{k}-t\triangledown f(x_k)-x^*||^2\\ &= ||x_{k}-x^*||^2-2t\triangledown f(x_k)(x_{k}-x^*)+t^2||\triangledown f(x_k)||^2 \\ \end{split}\]

因为\(t \triangledown f(x_k) = x_{k}-x_{k+1}\)

\[\triangledown f(x_k)(x_k -x^*) = \frac{1}{2t}( ||x_{k}-x^*||^2 - ||x_{k+1}-x^*||^2+ ||x_{k}-x_{k+1}||^2 ) \quad (1)\]

将左边的\(x_k\)换成\(x_k = x_{k+1}+t\triangledown f(x_k)\),该式可变为：

\[\triangledown f(x_k)(x_{k+1} -x^*) = \frac{1}{2t}( ||x_{k}-x^*||^2 - ||x_{k+1}-x^*||^2-||x_{k}-x_{k+1}||^2 ) \quad (2)\]

这就是欧式距离的\(Bregman Divergence\)的三点性质。【(2)对应SVRG++定理3.2】

若\(f(x)\)为凸函数，（2）式可写成：

\[f(x_{k+1})-f(x^*) \leq \frac{1}{t}(D(x_k,x^*)-D(x_{k+1},x^*)-D(x_k,x_{k+1}))\] \[f(x_{k+1})+ \frac{1}{t}(D(x_{k+1},x_k)+D(x_{k+1},x^*)) \leq f(x^*)+ \frac{1}{t}D(x^*,x_k)\]

该式对应这里引理1：

\[\phi (z^+) + D(z^+,z)+D(x,z^+) \leq \phi(x) + D(x,z)\]

其中\(z^+\)为\(z\)的下一步，\(x^*\)对应\(x\),然后即可推出mirror descent达到\(\epsilon\)误差需要\(\frac{LD(x^*,x_0)}{\epsilon}\),上篇文章收敛速度中推导出梯度下降:

\[f(x_k)-f(x^*) \leq \frac{||x_0-x^*||^2}{2tk}\]

达到\(\epsilon\)误差需要走\(\frac{\|x_0-x^*\|^2}{2t\epsilon}\)步,步长取\(t=\frac{1}{L}\),\(D\)取欧式距离，mirror descent收敛速度与GD收敛速度一样。

同样地，对于非光滑mirror descent用次梯度，需要步数：

\[k=\frac{L^2 \|x_0-x^*\|^2 }{2\epsilon^2} =\frac{2L^2D(x_0,x^*)}{\epsilon^2}\]