Primal Dual Problem | Tingting Liao

1. Fenchel-Legendre Duality

Fenchel Duality和Legendre变换本质上是一样的，只是从不同的角度去解释，它刻画的是函数斜率与截距之间的关系。

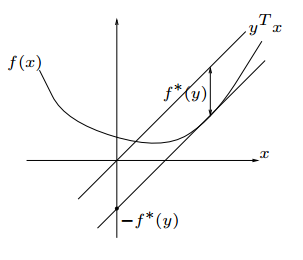过原点作一条斜线\(y=kx\)，将其向下平移与\(f(x)\)相切，该切线与\(y\)轴的截距与斜线向下平移的距离相等，\(f^*(k)是截距\):

\[f^*(k) = kx-f(x)\] \[f'(x)=k\]

这就是Legendre变换，Fenchel则将其换成一个更general的表达式：

\[f^*(y) = \max_x\{yx-f(x)\}\]

\(f^*(y)\)称为\(f(x)\)的共轭,这样的好处是，当\(f(x)\)是非凸函数时，\(f(x)=k\)不唯一，而Fenchel可以很好解决这个问题得到唯一解。

例：求\(g(x) = \log(1+e^x)\)的共轭\(g^*(y)\)

切线斜率\(y = \frac{e^x}{1+e^x} \in (0,1)\),\(e^x = \frac{y}{1-y},x = \log \frac{y}{1-y}\)
\[g(x)=\log(1+e^x)=\log \frac{1}{1-y}\]

\[\begin{split} g^*(y) &= yx-g(x) \\ &= y\log \frac{y}{1-y}-\log \frac{1}{1-y} \\ &= y\log y +(1-y) \log(1-y) \end{split}\] \[\therefore g^*(y)=\left\{\begin{matrix} y\log y +(1-y) \log(1-y) &\quad y\in (0,1)\\ 0 &\quad otherwise \end{matrix}\right.\]

Fenchel共轭的性质：

共轭的共轭等于原函数\(g^{**}(x) = g(x)\)
\(g(x)\)是凸函数，那么共轭\(g^*(x)\)也为凸函数
\(g(x)\)是\(L-smooth\),那么\(g^*(x)\)是\(\frac{1}{L}-SC(Strongly Convex)\)

2. Primal Dual

Primal

\[\min_{x \in R^d}{\Phi(x)+\frac{1}{n}\sum_{i=1}^{n}f_i(a_i x)} \quad (1)\]

Primal Dual
前一项不变（Primal），将后一项\(ERM\)换成对偶（Dual）形式：

\[\min_{x \in R^d}\max_{y \in R^d}{\Phi(x)-\frac{1}{n}\sum_{i=1}^{n}f^*_i(y) +\frac{1}{n}y^TAx } \quad (2)\]

Dual

将(2)式第一项与第三项替换合并为其对偶形式，那么整个目标函数就变成对偶问题：

\[\begin{split} &-\min_{x \in R^d}\max_{y \in R^d}{-\Phi(x)+\frac{1}{n}\sum_{i=1}^{n}f^*_i(y) -\frac{1}{n}yx } \\ =& -\min_{y \in R^d}{\Phi^*(-\frac{1}{n}A^Ty)+\frac{1}{n}\sum_{i=1}^{n}f^*_i(y) }\quad (3) \end{split}\]

例：求\(\frac{\sigma}{2} ||x||^2+\frac{1}{2n}\sum_{i=1}^n(a_i^Tx-b_i)^2\)的对偶问题。

该式对应Primal（1）式：

\[f(a_i^Tx) = \frac{1}{2}(a_i^Tx-b_i)^2\] \[f(z) = \frac{1}{2}(z-b_i)^2\]

下面求共轭\(f^*(y)\):

\[y =z-b_i,\therefore z = y+b_i,f(z)=\frac{1}{2}y^2\] \[\begin{split} f^*(y)&=yz-f(z) \\ & =y(y+b_i)- \frac{1}{2}y^2 \\ & = \frac{1}{2}y^2 + b_iy \end{split}\]

对应(2)式：

\[\frac{\sigma}{2} ||x||^2-\frac{1}{n}\sum_{i=1}^n(\frac{1}{2}y_i^2 + b_iy_i ) +\frac{1}{n}y^TAx \quad (Primal Dual)\]

下面计算Dual问题：

\[\Phi(x)= \frac{\sigma}{2} ||x||^2\] \[y=\sigma ||x||,\therefore ||x|| = \frac{y}{\sigma},\Phi(x)=\frac{y^2}{2\sigma}\] \[\begin{split} \Phi^*(y) &= y^Tx-\Phi(x) \\ & = \frac{y^2}{\sigma} - \frac{y^2}{2\sigma} = \frac{y^2}{2\sigma} \end{split}\] \[\Phi^*(-\frac{1}{n}A^Ty) =\frac{1}{2\sigma} ||\frac{A^Ty}{n}||^2\]

对应（3）式：

\[-\min_{y \in R^d}{\frac{1}{2\sigma} ||\frac{A^Ty}{n}||^2+\frac{1}{2n}||y||^2 +\frac{1}{n}y^Tb } \quad (Dual)\]

3. Stochastic Solvers

泽园大神总结了针对Primal,Primal-Dual,Dual问题的随机方法并将其分为三类：SGD,方差下降/随机下降和加速算法。

avatar

并针对四种情况，讨论各类方法的收敛性，这里只给出总结性结果不讨论方法具体实现过程。

Case1: 强突光滑。\(\sigma>0,L < +\infty.\)
Case2: 强突非光滑。\(\sigma>0,L = +\infty.\)
Case3: 非强突光滑。\(\sigma=0,L < +\infty.\)
Case4: 非强突非光滑。\(\sigma=0,L = +\infty.\)

3.1 SGD VS SVRG

	Case1	Case2	Case3	Case4
\(SGD\)	\(O(\frac{L^2}{\sigma \epsilon})\)	\(O(\frac{G}{\sigma \epsilon})\)	\(O(\frac{L^2}{ \epsilon^2})\)	\(O(\frac{G}{ \epsilon^2})\)
\(SVRG\)	\(O((n+\frac{L}{\sigma})\log\frac{1}{\epsilon})\)		\(O(n\log\frac{1}{\epsilon}+\frac{L}{\epsilon})\)

\(SVRG\)在函数光滑的情况下比\(SGD\)快，而在非光滑的情况下比\(SGD\)多了\(O(n)\).

3.2 Stochastic Dual Coordinate ascent(SDCA)

coordinate descent坐标下降的两条定理：

如果目标函数为\(L-smooth\),收敛速率为\(O(\frac{nL}{\epsilon})\)
如果目标函数为\(\sigma-StronglyConvex\),收敛速率为\(O(\frac{nL}{\sigma}\log\frac{1}{\epsilon})\)

值得注意的是，对于一个Primal问题使用\(SVRG\)，将其转换成Dual问题使用坐标下降，两者的收敛速度是一样的吗？答案是一样的。
假设原始问题中\(\Phi(x)\)是\(\sigma-SC\),\(f(x)\)是\(L-smooth\)：

\[\min_{x \in R^d}{\Phi(x)+\frac{1}{n}\sum_{i=1}{n}f_i(a_i x)} \quad (1)\]

那么\(\Phi^*(x)\)是\(\frac{1}{\sigma}-smooth\),\(f^*(x)\)是\(\frac{1}{L}-SC\),其对偶：

\[g(y) = {\Phi^*(-\frac{1}{n}A^Ty)+\frac{1}{n}\sum_{i=1}^{n}f^*_i(y) }\]

\(g(y)\)是\((\frac{1}{n^2\sigma}+ \frac{1}{nL})-smooth\),\(\frac{1}{nL}-SC\),代入到第二条定理中:

\[\begin{split} &O(\frac{dL}{\sigma}\log\frac{1}{\epsilon}) \\ =& O( \frac{n (\frac{1}{n^2\sigma}+ \frac{1}{nL})}{\frac{1}{nL}}\log\frac{1}{\epsilon}) \\ =& O((n+\frac{L}{\sigma} )\log\frac{1}{\epsilon}) \end{split}\]

可以看到在凸且光滑的情况下，\(SDCA\)与\(SVRG\)的收敛速度相等，而在另外三种情况下它们也等价。

3.3 Accelerated Proximal Coordinate Gradient (APGC)

\(APGC\)在\(SDCA\)的基础上用了Neterov Momentum加速算法.SDCA收敛速度为\(O(\frac{nL}{\sigma}\log\frac{1}{\epsilon})\),\(APCG\)收敛速度为\(O(\frac{n\sqrt{L}}{\sqrt{\sigma}}\log\frac{1}{\epsilon})\)

	Case1	Case2	Case3	Case4
\(SDCA\)	\(O(n+\frac{L}{\sigma})\)	\(O(n+\frac{G}{\sigma\epsilon})\)	\(O(n+\frac{L}{\epsilon})\)	\(O(n+\frac{G}{\epsilon^2})\)
\(APCG\)	\(O(n+\frac{\sqrt{nL}}{\sqrt{\sigma}})\)	\(O(n+\frac{\sqrt{nG}}{\sqrt{\sigma\epsilon}})\)	\(O(n+\frac{\sqrt{nL}}{\sqrt{\epsilon}})\)	\(O(n+\frac{\sqrt{nG}}{\epsilon})\)

可以看到\(APCG\)比\(SDCA\)收敛更快，加速算法总是比非加速算法快的。

3.4 Stochastic Primal Dual Coordinate (SPDC)

\(SPDC\)主要针对Primal-Dual，也就是说它需要更新两方面的参数，一方面用坐标下降更新Dual问题一方面用SVRG更新Primal问题：

coordinate descent： \(y_{k+1} = y_k-\eta_y \triangledown g_i(y)\)
full gradient descent: \(x_{k+1} = x_k-\eta_x \triangledown g(x)\)

并且需要保存两个学习率\(\eta_y,\eta_x\).\(SPDC\)的主要贡献在于它使用了momentum，它的收敛速率和\(APCG\)相等。

3.5 Katyusha

Katyusha是针对原始问题随机梯度方法的加速方法，有一个问题是Momentum不能直接用在SGD中，这是因为SGD的gradient方向本身就不够准确，而用momentum过后之前不够准确的梯度方向会进一步导致后面的梯度方向往错的方向走。

泽园大神的Katyusha就很巧妙，负梯度（黑线）–> momentum（绿线）–> retracted（黄线）–> 负梯度方向 –> momentum–> retracted…

它在momentum的基础上增加了一步retracted过程，即momentum点与起始点\(x_0\)相连取中点为最后更新的位置，在一次epoch过后将最终点设为新的起始点\(x_o\)去retracted后面更新的点。

Katyucha的收敛速度与SPDC和APCG的收敛速度相等。

4. 总结

1.如何选择Primal、Primal-Dual和Dual问题？

Case1: \(\Phi(x)\)强凸\(f(x)\)光滑，可以选择Primal或Dual，不推荐Primal-Dual，因为它需要调整两个学习率.
Case2: \(\Phi(x)\)强凸\(f(x)\)不光滑，对偶目标函数是光滑非强凸，推荐Dual问题不推荐原始问题。
Case3：原始问题中\(\Phi(x)\)非强凸\(f(x)\)光滑，推荐Primal不推荐Dual，因为对应的Dual的目标函数是不光滑强凸的，而coordinate descent要求函数光滑，如果要用需要先
Case4：Primal和Dual的目标函数都是非强凸非光滑的，推荐Primal-Dual。
其它更复杂的情况，如\(f(x)\)是非凸，或者不是\(f(a_i^Tx)\)的形式，推荐使用Primal而不用Dual，因为Dual问题可能会变得十分高维。

2. 什么时候用加速算法？

当\(\epsilon\)特别小的时候。即对结果精度要求特别高的时候可以用加速算法。
当\(\sigma\)特别小的时候。因为当\(\sigma\)特别小的时候，加速算法的收敛速度会比非加速算法快特别多。

3.并行计算Mini-Batch