差分隐私-三种机制

1. 基础知识介绍

差分隐私主要目的是最大化utility的查询结果同时保证个人隐私的泄露不超过\(\epsilon\).

1.1 概括

• 差分隐私主要包含以下两类：
  1. 中心化差分隐私(\(\epsilon-DP\))
  2. 本地化差分隐私(\(\epsilon-LDP\))

其区别在于中心化差分隐私的随机函数运行于服务器上，而本地化差分隐私的运行于本地。服务器上数据有全局敏感性，而本地查询中任意用户之间并不知晓其它人的数据记录。因此中心化差分隐私一般采用拉普拉斯、指数噪声机制等方法，而本地化差分隐私主要采用随机响应技术保护隐私。

• 加噪方法主要分为以下两类：
  1. 扰动（perturbation）
     • 对输入数据扰动：随机响应（Randomized Response）
     • 对输出数据扰动：拉普拉斯算法（Laplace）
     • 中间数据：随机响应或拉普拉斯算法
  2. 采样（sampling）
     该算法中心思想为：将数据集分为\(k\)份，对每份数据应用拉普拉斯或随机相应算法。它的好处是对小数据集进行处理从而提高运行效率，有点类似于随机梯度下降计算每个Batch的梯度。

1.2 差分隐私

核心思想：对于差别只有一条记录的两个相邻数据集，查询它们获得相同值的概率非常接近。

\[P[M(D)\in S] \leq e^\epsilon P[M(D')\in S] \\ \frac{P[M(D)=S]}{P[M(D')=S]} \leq e^{\epsilon}\]

对于两个只相差一个记录的相邻数据集\(D\)和数据集\(D'\),查询算法\(M\)的输出结果\(S\)的概率应该非常接近。对于任意参数\(\epsilon >0\),函数\(M\)满足\(\epsilon-differential \quad privacy\) \(\epsilon\)接近于0，两个概率接近相等，保密程度高，噪声越大 \(\epsilon\)越大，数据越准确，保密程度低，噪声越小。

1.3 组合定理Composition Theorem

• 串行组合 (Sequential Composition)
  假设有\(k\)个算法\(M_1, M_2, …, M_k\)在同一数据库\(D\)上进行差分隐私算法, \(M_i\) 满足\(\epsilon_i\) 差分隐私,这样在顺序执行这些算法之后,那么组合后的算法满足\(\sum_i \epsilon_i-DP\):

\[\epsilon = \epsilon_1 +\epsilon_2+...+\epsilon_k\]

• 并行组合 (Parallel Composition)
  假设有\(k\)个算法\(M_1, M_2, …, M_k\)分别作用于数据集\(D_1, D_2, …, D_k\)上,\(M_i\) 满足\(\epsilon_i\)差分隐私,那么组合后算法满足\(\max\epsilon_i\)-差分隐私:

\[\epsilon_i = \max\{ \epsilon_1 ,\epsilon_2,...,\epsilon_k \}\]

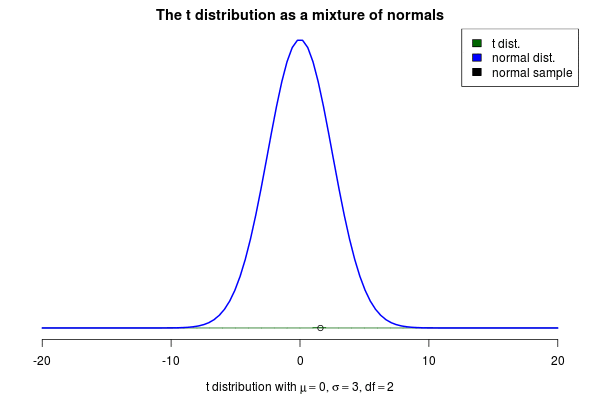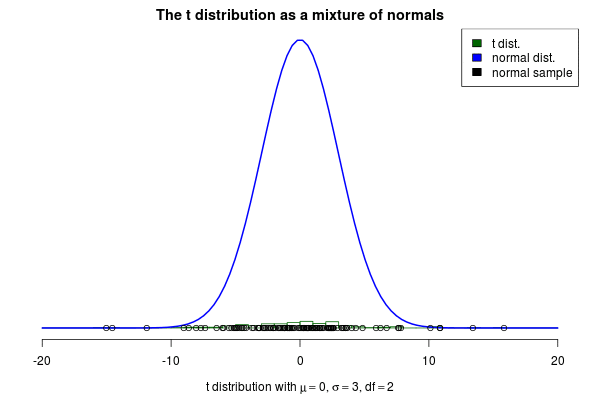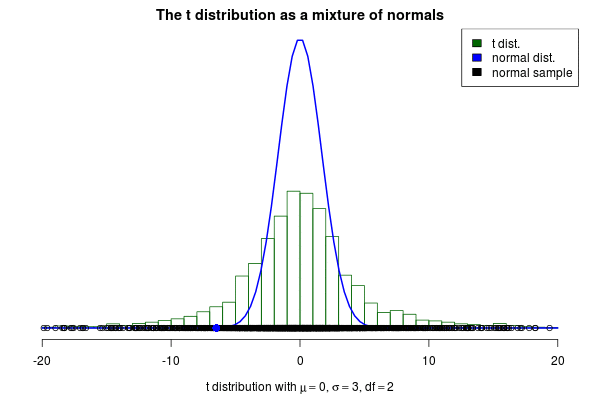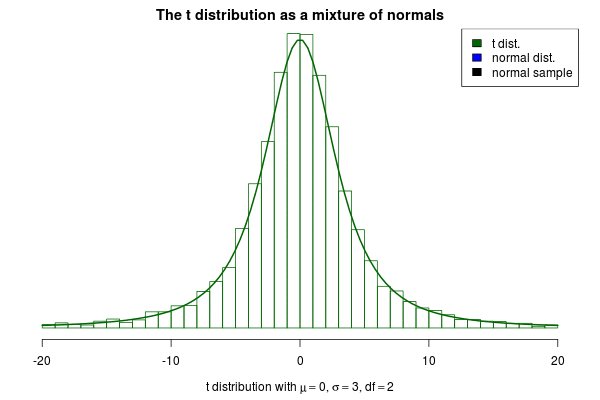
2. 三种分布

\(\quad\quad\quad f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{\sigma^2}} \quad\quad\quad\quad f(x)=\frac{1}{2\lambda}e^{-\frac{|x-\mu|}{\lambda}}\quad\quad\quad f(x)=\left\{\begin{matrix} \lambda e^{-\lambda x} &x>0 \\ 0 &x\leq 0 \end{matrix}\right.\)

	Gaussian	Laplace	Exponential
\(X \sim\)	\(N(\mu,\sigma)\)	\(L(\mu,\lambda)\)	\(E(\lambda)\)
\(E(X)\)	\(\mu\)	\(\mu\)	\(\frac{1}{\lambda}\)
\(D(X)\)	\(\sigma\)	\(2\lambda^2\)	\(\frac{1}{\lambda^2}\)
\(sensitivity\)	\(l_2\)	\(l_1\)	\(l_1\)
加噪对象	数值型	数值型	非数值型

以高斯分布为例，可以把概率看作是点到均值的距离，距离中心点越远概率越小，距离越近概率越大。

\[D_{Gau} = ||x-\mu||_2\] \[D_{Lap} = ||x-\mu||_1\] \[D_{Exp} = \lambda x\]

其中拉普拉斯用一范式距离，高斯是二范式即欧式距离，分别对应了differential privacy中的\(l_1,l_2-sensitivity\).而\(\frac{x-\mu}{\sigma}\)是为了归一化，可以看作是统一量纲消去变量之间的，例如在二元高斯中特征\(X=[x_1,x_2]\)表示身高和体重,而身高和体重之间的量纲是不一样的,直接计算距离会产生很大的误差，那么就需要对其归一化再计算其总距离：

\[Distance = \frac{(x_1-\mu_1)^2}{\sigma_1^2}+\frac{(x_2-\mu_2)^2}{\sigma_2^2}\]

再用指数函数放大距离，即放大距离对概率的影响。而前面的系数则是为了积分等于1.例如：

\[\int e^{-\frac{(x-\mu)^2}{\sigma^2}} = {\sqrt{2\pi}\sigma}\]

拉普拉斯分布和指数分布同理。

3. Laplace机制

Definition 1 \((l_1-sensitivity\))：查询函数\(f\)的\(l_1\)敏感度表示相邻数据集输出的最大\(l_1\)距离。

\[\Delta f = \max_{D,D'}||f(D)-f(D')||_1\]

Theorem 1 \((Laplace Mechanism)\)：

\[M(D) = f(D)+Y\]

Definition 3：噪声\(Y \sim L(0,\frac{\Delta f}{\epsilon})\)满足\((\epsilon,0)-differential　privacy.\)

证明：

\[\begin{split} & \ln \frac{P[M(D)=S]}{P[M(D')=S]} \\ = &\ln\frac{\frac{\epsilon}{2\Delta f}e^{ \frac{\epsilon}{\Delta f}|f(D)|}}{ \frac{\epsilon}{2\Delta f}e^{ \frac{\epsilon}{\Delta f}|f(D')|}}\\ =&{\frac{\epsilon}{\Delta f}(|f(D)|-|f(D')|)} \leq {\epsilon} \\ \therefore需满足&\quad |f(D)|-|f(D')| \leq \Delta f \\ &\quad |f(D)|-|f(D')| \leq \max_{D,D'}|f(D)-f(D')| \end{split}\]

该式满足绝对值不等式，因此\(Laplace(0, \frac{\Delta f}{\epsilon})\)满足\(\epsilon-\)差分隐私。

4. Gaussian机制

Definition 1 \((l_2-sensitivity\))：查询函数\(f\)的\(l_1\)敏感度表示相邻数据集输出的最大\(l_2\)距离。

\[\Delta f = \max_{D,D'}||f(D)-f(D')||_2\]

Theorem 1 \((Laplace Mechanism)：\)对于任意的\(\delta\in(0,1),\sigma>\frac{\sqrt{2ln(1.25/ \delta)}\Delta f}{\epsilon}\),有噪声\(Y \sim N(0,\sigma^2)\)满足\((\epsilon,\delta)-differential　privacy.\)

\[P[M(D)\in S] \leq e^\epsilon P[M(D')\in S]+\delta\] 证明： \[\begin{split} &|ln \frac{e^{-\frac{1}{2\sigma^2}x^2}}{e^{-\frac{1}{2\sigma^2}(x+\Delta f)^2}}|\\ =&| {\frac{1}{2\sigma^2}(2x\Delta f+(\Delta f)^2)}| \leq \epsilon \\ \therefore \quad |x| \leq \frac{\sigma^2\epsilon}{\Delta f}-\frac{\Delta f}{2} \end{split}\]

令\(t=\frac{\sigma^2\epsilon}{\Delta f}-\frac{\Delta f}{2}\),当且仅当\(\|x\|\leq t\)时，该分布是满足DP的，而当\(\|x\|>t\)时为隐私泄露，我们希望隐私泄露的概率小于\(\delta\),即：

\[P(|x|>t)<\delta\] \[P(x>t)<\frac{\delta}{2}\]

正太分布的上下界证明可参照这里. 以下证明其上界：

\[\begin{split} P(x>t) &= \frac{1}{\sqrt{2\pi}\sigma}\int_t^\infty e^{-\frac{x^2}{2\sigma^2}}dx \\ &< \frac{1}{\sqrt{2\pi}\sigma}\int_t^\infty \frac{x}{t} e^{-\frac{x^2}{2\sigma^2}}dx \quad 【因为x>t】\\ &=\frac{\sigma}{\sqrt{2\pi}t}e^{-\frac{t^2}{2\sigma^2}} \end{split}\]

那么问题转变为：

\[\begin{split} \frac{\sigma}{\sqrt{2\pi}t}e^{-\frac{t^2}{2\sigma^2}} &< \frac{\delta}{2} \\ \frac{t}{\sigma}e^{\frac{t^2}{2\sigma^2}} &> \frac{2}{\sqrt{2\pi}\delta} \\ \ln \frac{t}{\sigma} + \frac{t^2}{2\sigma^2} &> \ln\frac{2}{\sqrt{2\pi}\delta} \end{split}\] \[\begin{split} 将该式转换为\left\{\begin{matrix} \ln \frac{t}{\sigma} & \geq 0\\ \frac{t^2}{2\sigma^2} & > \ln\frac{2}{\sqrt{2\pi}\delta} \end{matrix}\right. \end{split}\]

下面分别分析左边两项，由于\(t=\frac{\sigma^2\epsilon}{\Delta f}-\frac{\Delta f}{2}\)，若令\(\sigma=c\frac{\Delta f}{\epsilon}\),那么\(t=c\sigma-\frac{\Delta f}{2}\),因此：

\[\frac{t}{\sigma} = c-\frac{\Delta f}{2\sigma} = c-\frac{\epsilon}{2c}\]

这里\(\epsilon<1,c\geq 1,\)

\[\ln(c-\frac{\epsilon}{2c}) > \ln(c-\frac{1}{2})\geq 0\] \[\therefore c\geq\frac{3}{2}\]

第二项：

\[\begin{split} \frac{t^2}{2\sigma^2} &=\frac{1}{2}(c-\frac{\epsilon}{2c})^2 \\ &= \frac{1}{2}(c^2-\epsilon + \frac{\epsilon^2}{4c^2}) \end{split}\]

因为\(\epsilon<1,c\geq\frac{3}{2}\),

\[\begin{split} c^2-\epsilon + \frac{\epsilon^2}{4c^2} > c^2 - \frac{8}{9} > 2\ln\frac{2}{\sqrt{2\pi}\delta} \end{split}\] \[c^2 > \ln\frac{2}{\pi}e^{\frac{8}{9}}+2\ln\frac{1}{\delta}\] \[\because \ln\frac{2}{\pi}e^{\frac{8}{9}}>1.25^2\] \[\therefore c^2>2\ln\frac{1.25}{\delta}\]

上文中我们令\(\sigma=c\frac{\Delta f}{\epsilon}\),因此\(\sigma>\frac{\sqrt{2\ln(1.25/ \delta)}\Delta f}{\epsilon}\).随机梯度下降中\(\sigma \geq c\frac{q \sqrt{T \ln(1/\delta)}}{\epsilon}\)【下次再证】。

5. 指数机制

Definition 1 选择一个查询\(r\),给定分值函数（score function）,指数机制以\(M(x,q,r)\)的概率输出结果\(x\)

\[M(x,q,r) = e^{\frac{\epsilon q(x,r)}{2\Delta q}}\] \[\Delta q = \max_{x,x'}||q(x,r)-q(x',r)||\]

Theorem 1 指数分布\(E( \frac{\epsilon}{2\Delta q})\)满足\(\epsilon-DP\).

证明：

\(\quad\)这里是以一个概率输出结果，不是直接对数值数据进行加噪，因此需要归一化以概率表示：

\[\begin{split} \frac{P[M(x,q,R)=r]}{P[M(x',q,R)=r]} &= \frac{\frac{ e^\frac{\epsilon q(x,r)}{2\Delta q}}{\sum_R e^\frac{ \epsilon q(x,R)}{2\Delta q}}}{\frac{ e^\frac{\epsilon q(x',r)}{2\Delta q}}{\sum_R e^\frac{ \epsilon q(x',R)}{2\Delta q}} } \\ & = \frac{e^\frac{\epsilon q(x,r)}{2\Delta q}}{e^\frac{\epsilon q(x',r)}{2\Delta q}} \frac{\sum_R e^\frac{\epsilon q(x',R)}{2\Delta q}}{\sum_R e^\frac{\epsilon q(x,R)}{2\Delta q}} \end{split}\]

第一项

\[e^{\frac{\epsilon}{2\Delta q}(q(x,r)-q(x',r))} < e^{\frac{\epsilon}{2}}\]

第二项

\[\frac{\sum_i e^\frac{\epsilon q(x',R_i)}{2\Delta q}}{\sum_i e^\frac{\epsilon q(x,R_i)}{2\Delta q}} = \frac{\sum_i e^\frac{\epsilon q(x,R_i)}{2\Delta q} e^\frac{\epsilon (q(x',R_i)-q(x,R_i))}{2\Delta q}} {\sum_i e^\frac{\epsilon q(x,R_i)}{2\Delta q}}\] \[\because e^\frac{\epsilon (q(x',R_i)-q(x,R_i))}{2\Delta q}\leq e^{\frac{\epsilon}{2}}\] \[\therefore \frac{\sum_i e^\frac{\epsilon q(x',R_i)}{2\Delta q}}{\sum_i e^\frac{\epsilon q(x,R_i)}{2\Delta q}} \leq e^{\frac{\epsilon}{2}}\] \[\therefore \frac{P[M(x,q,R)=r]}{P[M(x',q,R)=r]} \leq e^{\epsilon}\]

因此\(E( \frac{\epsilon}{2\Delta q})\)满足\(\epsilon-differential　privacy\).